
Figure 1.29: This is not natural. (Copyright © 2009 Becky Northey, Pooktre CC BY 3.0)
Plants are topologically relatively simple. The upper parts of plants are essentially never toroidal except in cases of human intervention.

Figure 1.30: This is uncommon. It is called inosculation or cojoining. In this picture two different trees have naturally joined together by getting really close and rubbing against eachother. (Copyright © 2009 Roger Griffith CC0 Public Domain)
The roots, however, may be toroidal and graph-like.

Figure 1.31: This tree’s roots have grown together (self grafted in the terminology of botinists) into a toroidal graph-like structure (Copyright © Lisa McCarty CC0 1.0 Public Domain)
Why would roots be toroidal and graph-like when above ground branches are not? I would posit that roots are less dispensable and less replaceable than branches and leaves. Roots probably contain more nutrients and are probably harder to grow. More importantly, when a branch dies and falls off, it falls to the ground, getting out of the way. And even if it doesn’t fall to the ground, there is usually quite a lot of empty air-space around the plant for the plant to grow a new branch into. The ground has less space in it, and the old dead root is likely to get in the way. So it is important to plants that parts of their root system don’t become disconnected from the rest of the plant by way of being cut. If I cut a branch of a tree then all of the sub-branches and leaves attached to that branch become disconnected from the rest of the tree. If I cut a root, which is connected to other roots in a toroidal and graph-like fashion, the tree may lose one pathway to get nutrients in and out of that section of it’s root system, however it won’t lose all of its pathways. In network theory and graph theory this property of graphs is called path redundancy and is a fundamental mathematical advantage to graph-like systems and structures. It is also a slight disadvantage over the tree, as quarantining a diseased root requires blocking off multiple pathways, where-as the quarantining of a diseased branch requires blocking off only one edge-vertex connection.
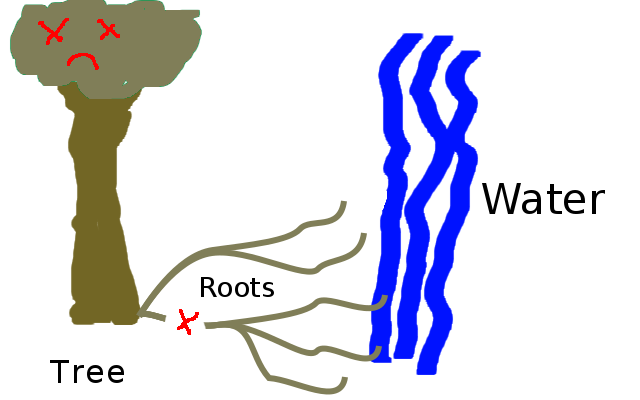
Figure 1.33: It only takes cutting a tiny section of root for the tree to lose its connection to the water supply. (Copyright © 2016 Timothy Hobbs CC BY-SA 4.0)
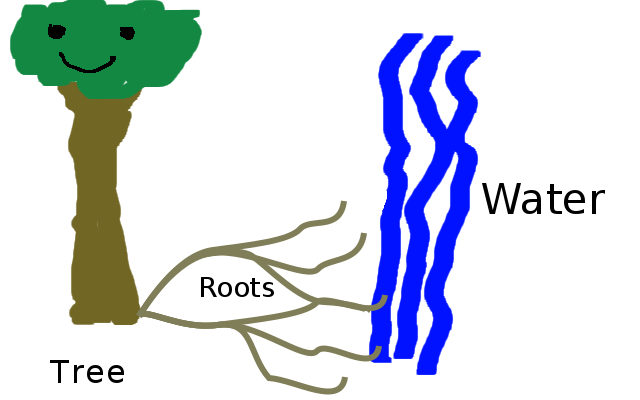
Figure 1.34: If the roots connect to each-other to form a graph-like structure then there is path redundancy between the roots that reached water and the tree. (Copyright © 2016 Timothy Hobbs CC BY-SA 4.0)
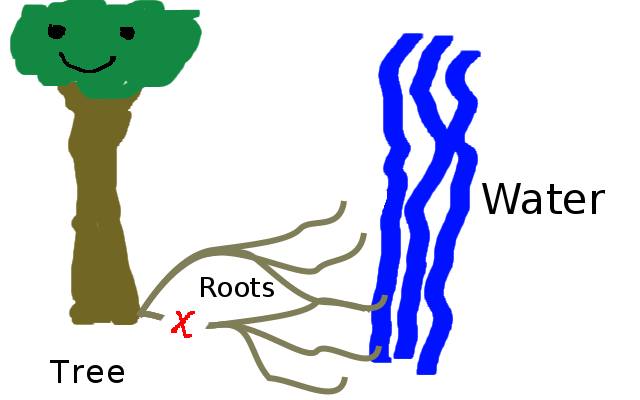
Figure 1.35: You have to cut more than one section of root in order to break the trees connection to water. (Copyright © 2016 Timothy Hobbs CC BY-SA 4.0)
These structures are not, however, true graphs, as discrete vertexes and edges cannot be easily identified.
Beyond self grafting for the purposes of redundancy, relatively recent research has shown that trees also transfer nutrients and communicate with each-other through their roots. This lecture by tree ecologist Suzanne Simard is enlightening to the lay-person:
Figure 1.36: TED talk about the mycorrhizal networks which connect trees. <https://www.ted.com/talks/suzanne_simard_how_trees_talk_to_each_other> (Copyright © 2O16 Suzanne Simard CC BY-NC-ND 3.0)
In these networks trees transfer nutrients and potentially hormonal information(not yet proven) via fungi which connect to their roots. Like molecules, which I described as being an amorphous blob of electroniness with nuclii stuck in the middle, in these graphs of trees, it is much easier to distinguish the vertexes than the edges. I would say that the vertexes are discrete but the edges are not.
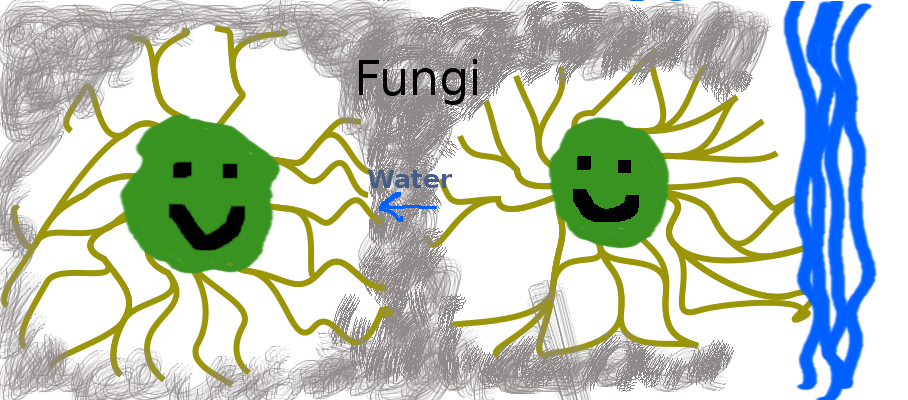
Figure 1.37: The tree on the left gets water from the tree on the right via the fungi network connecting the trees. (Copyright © 2016 Timothy Hobbs CC BY-SA 4.0)
This kind of nutrient transfer is vital to the forests survival. When a young tree is growing up, its branches are not yet tall enough to reach the sun. Without this "nutrient communism" it would be impossible for trees in forests to reproduce, because the young trees would all be shaded out and die of "starvation". It has also been shown that this tree communism helps forests survive droughts. Trees which are near water send water through the root network to other trees which are thirsty. From each according to their means, to each, according to their needs.
And now things get really exciting.
The nervous system is a graph. When I say that I don’t just mean the human brain, I’m referring to all multi-neuron nervous systems.
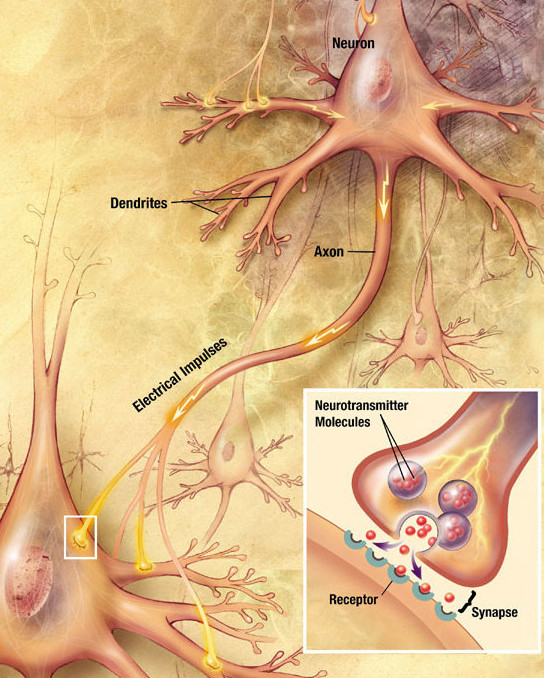
Figure 1.39: Neurons connect to each-other via discrete edges called dendrons as drawn. (Copyright © 2009 US National Institutes of Health Public Domain)
Nervous systems are made up of neurons. These are cells like any other. They have a nucleus, a cell wall, and some fluid inside with lots of other stuff that isn’t important to this work. They are funnily shaped however. They certainly aren’t bloby like this amoeba.
Figure 1.40: A photograph of an amoeba, which is a bloby single celled organism. (Copyright © 1907 Unknown Public Domain)
Neurons are more like blobs with tree-like appendages. However, when we look at a graph of neurons we can clearly identify the neuron cell nuclei as being the vertexes and the dendrons (their tree-like appendages) as being the edges! While the molecule and the communist tree-root network have amorphous edges and discrete vertexes both the edges and the vertexes of the nervous system are almost fully discrete.
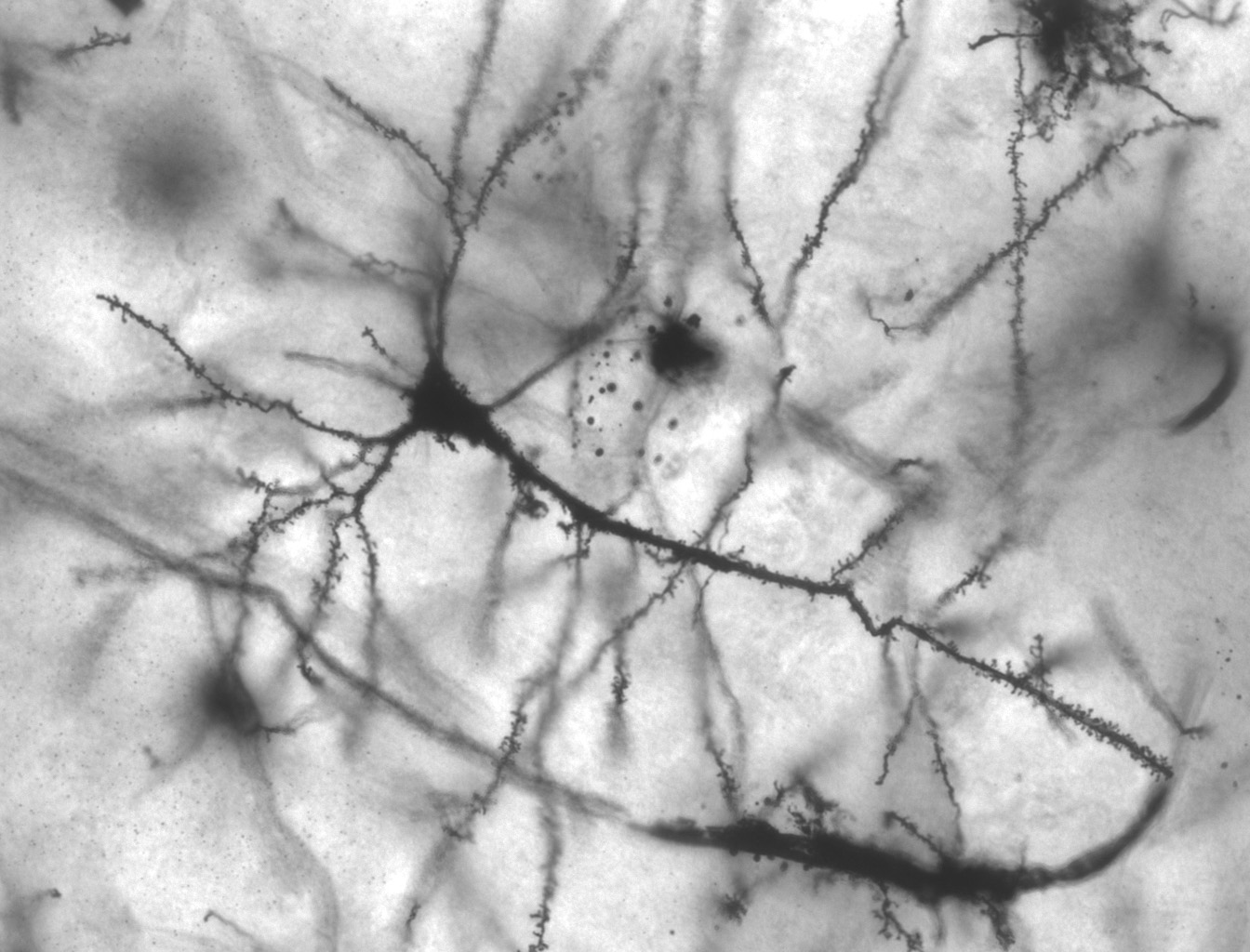
Figure 1.41: A photograph of a pyramidal neuron in the hippocampus (Copyright © 2005 MethoxyRoxy CC BY-SA 2.5)
The nervous system is the closes thing to a fully discrete graph that exists in the natural world. It is no coincidence, that the graphiest structure that exists also has the most interesting behavior. In the next chapter I will discuss graph based systems, how they differ from mere structures, and also some of their properties and classification. In the mean time, lets review some of the concepts that we learned in this chapter.