
Figure 1.21: Socotra dragon tree, Socotra island, Yemen (Copyright © 2008 Boris Khvostichenko CC-By-SA 4.0)
With the appearance of multi-celled life, the quantity and diversity of tree-like structures exploded.

Figure 1.21: Socotra dragon tree, Socotra island, Yemen (Copyright © 2008 Boris Khvostichenko CC-By-SA 4.0)
Indeed, multi-celled life forms tend to have at least several tree-like appendages and it is rare for a life form to be truly bloby. This is completely different from the non-biological world, which is mostly bloby and rarely tree-like.

Figure 1.22: Even bloby life forms like this slug have appendages. (Copyright © 2006 Guillaume Brocker CC BY-SA 3.0)

Figure 1.23: Rocks, however, almost never have appendages. (Copyright © 2012 Reptonix free Creative Commons licensed photos CC-By 3.0)
There must be something truly special about being tree-like, for life to have evolved to have such an unusual geometry. When I ask myself, "why does life need to be so tree-like?" my first impression is that it is hard to move if you’re a blob. However, plants don’t move, and they are even more treeish than animals are. Perhaps it is merely a side-effect of some property of growth. Further analysis shows, that the advantages and disadvantages of tree-like structures are diverse and that there are multiple competing factors in the shape of a plant or animal.
Animals tend to be bloby with only the few, relatively short, appendages which they need for locomotion or dexterity.
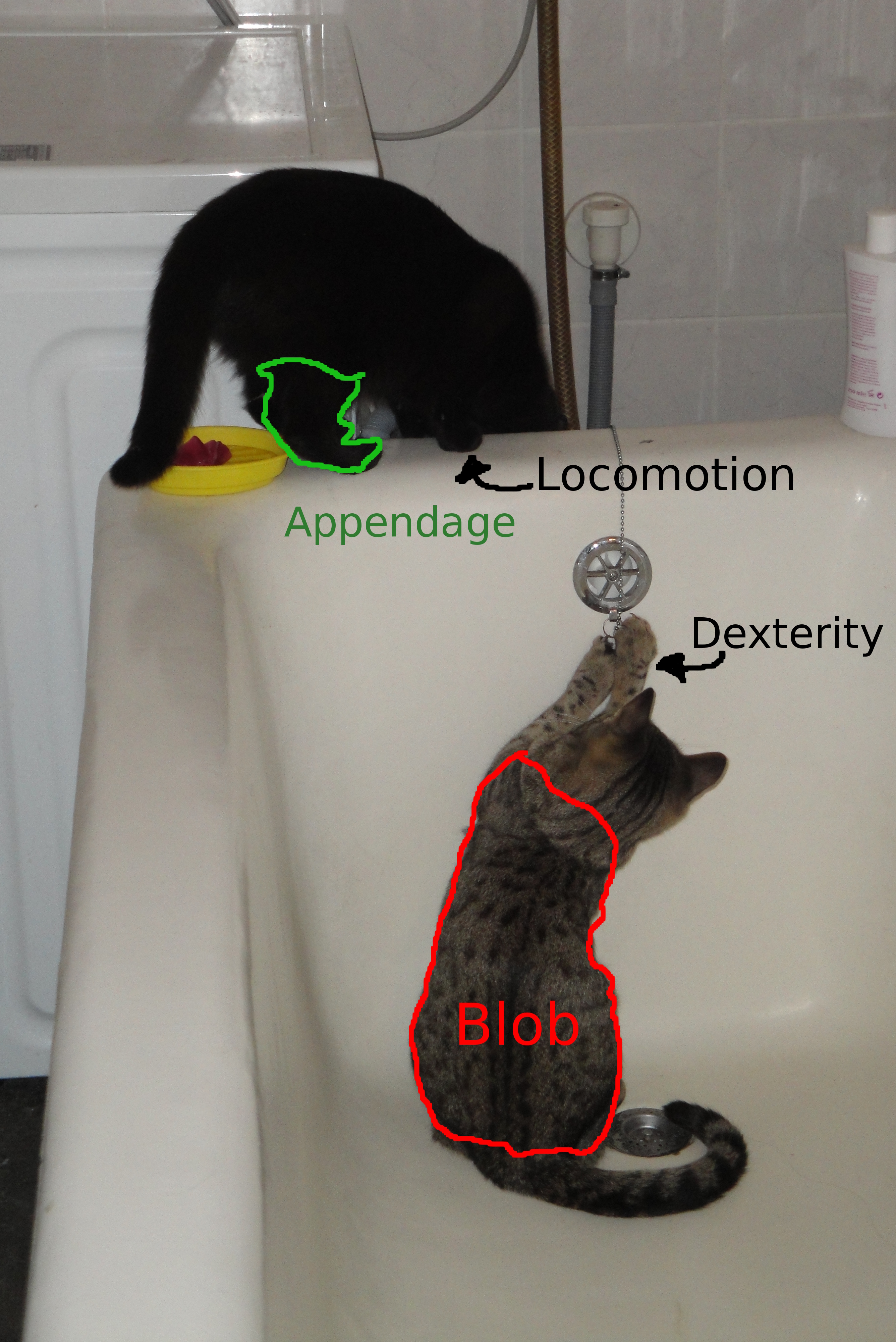
Figure 1.24: Two young mammamalian blobs exhibiting the use of their appendages for locomotion and dexterity. (Copyright © 2015 Denisa Hobbs CC BY-SA 4.0)
You will notice that the rock in Figure 1.23 is not just bloby, but downright round. It has been polished by tumbling in a stream. If it ever had a narrowish appendage, that appendage is long gone. Indeed, the key reason why rocks are almost exclusively bloby is that graph-like and tree-like structures are fragile!

Figure 1.25: An Eastern Box Turtle, pretending to be bloby, hiding in its shell to protect its fragile appendages(Copyright © 2011 Robin Baranowski, National Parks Service photo CC BY-SA 2.0)
The equation for heat loss of an organism is a product of its surface area. The shape with the lowest surface area per volume is a sphere. Anything other than a sphere loses unnecessary heat and appendages have a particularly high surface area to volume ratio.
Note: plants do not generate significant heat with their metabolisms and therefore are not evolutionarily motivated to conserve internally generated heat.
A very similar equation also applies to water loss. Plants are effected by this too.
One important thing to understand, is that an analysis of emperical data regarding the heat loss or water-loss of an organism is meaningless when studying the merits of biological geometry! For example, animals will send less blood to their limbs in order to combat heat loss. Emperically, this means that heat loss from limbs is relatively low in terms of heat loss per surface area. However, this is only an evolutionary adaption to a fundamental disadvantage to having a certain geometric shape. The same applies with water loss.
For animals:
For plants (in order of importance):
If an animal bights off a leaf, then a new leaf can be easily grown back. If, in the winter, temperatures are too low for leaf cells to survive, than these leaves can be grown back in the spring.
Having a tree-like structure allows plants to be tall cheaply. They do not need to invest much growth volume into growing high above their neighbors and therefor reaching the sun.
If a leaf or branch becomes infected, the plant can quarantine just the infected branch and survive.
Plants actually move towards the light, albeit slowly. Being long and thin allows them to do this.

Figure 1.26: A rose branch exhibiting winter dieback. Note that branches 2 and 4 are dead and have been quarantined by the plant to prevent the spread of disease. (Copyright © 2016 Timothy Hobbs CC BY-SA 4.0)
Near the beginning of this manual, I noted that the water surrounding the archipelago in Figure 1.5 is not a true graph because the vertexes and edges are not distinct. The rose bush in Figure 1.26 is a true tree in the mathematical sense. The vertexes and edges are very distinct. In the language of mathematics one would say that they are discrete. This discreteness plays a very important role in the reason why plants are geometrically tree-like.
The ability for the plant to treat leaves and branches as dispensable is dependent on its treatment of these leaves and their associated branches as discrete entities. When a person gets a deep gash in their finger, the wound will take months to heal, their finger will never be "like new" and the risk of fatal sepsis(blood poisoning) is severe. But you can tear a leaf on a plant to shreds and the plant will sabotage the leaf and grow a perfect new one in a fraction of the time it took the human to do a poor repair job. Furthermore, if an infection does occur in the leaf, and that infection begins to spread, the plant can choose a vertex bellow the infection point and sabotage an entire branch, as is illustrated in Figure 1.26.
Height is also an important reason why plants evolved to be tree-like and it might be even more important than the property of dispensability. Take a look at this cactus and tell me that it isn’t bloby.

Figure 1.27: A bloby Golden Barrel Cactus (echinocactus grusonii), Koko Crater Botanical Garden, Oahu Hawaii (Copyright © 20O9 Drew Avery CC BY 2.0)
The cactus needs to fight water loss and therefore tries to be spherical in order to minimize surface area. It deals with the lack of dispensability of its leaves by protecting itself with spikes having a thick skin. Its need for quarantinability is lessened by the fact that in dry climates infections are less likely. Its need to be tall is limited as there are few neighboring plants to compete with in the desert. Many cacti, rather than being a perfect spheres, are somewhat elongated in order to regain at least some of that lost hight advantage, however, this one is not.
Now compare that cactus to the trees in this forest, where height competition is at its peek. The trees have grown very tall, and certainly have branches in order to reach out into whatever ray of sunlight the can find.

Figure 1.28: A forest trail in H. Dutlinger Natural Area (Copyright © 2013 Nicholas A. Tonelli CC BY 2.0)
One thing I notice when I look at these trees though, is that they are less tree-like than the rose bush, both geometrically and in terms of graph-theory. Everything seems to come out of one central trunk and the sub-branches are not nearly as distinct. I have rarely seen a pine tree quarantine a sub-branch. They choose to drop entire branches instead. This lack of discreteness can probably be traced to the fact that few animals can reach up high enough to graze on the needles, and the tough needles are hardly worth eating anyways. The trees have found an alternative to discreteness and dispensability for their survival.